Coursera: Machine Learning (Week 8) Quiz - Principal Component Analysis | Andrew NG

 

 Recommended Courses:

1. Coursera: Machine Learning
2. Google Data Analytics Professional Certificate.

2.Principal Component Analysis.

Don't just copy & paste for the sake of completion. The solutions uploaded here are only for reference.They are meant to unblock you if you get stuck somewhere.Make sure you understand first.

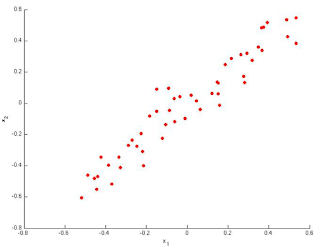
1. Consider the following 2D dataset:
   
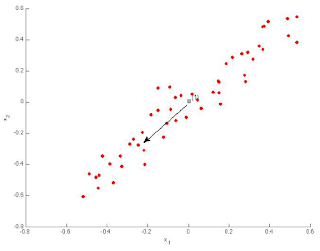
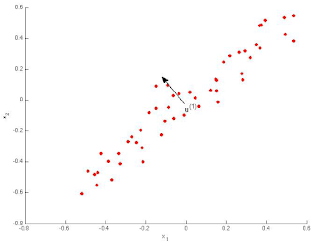
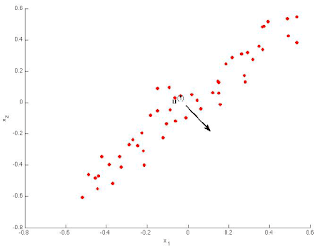
   Which of the following figures correspond to possible values that PCA may return for  (the first eigen vector / first principal component)? Check all that apply (you may have to check more than one figure).
   
   
   •  Figure 1:_1,2
           ANSWER:-1,2
   •  Figure 2:
     
   •  Figure 3:
     
   
   
   •  Figure 4:
     

---

2. Which of the following is a reasonable way to select the number of principal components k?
   (Recall that n is the dimensionality of the input data and m is the number of input examples.)
   
   
   •  Choose k to be the smallest value so that at least 99% of the variance is retained.
   
   
   •  Choose k to be the smallest value so that at least 1% of the variance is retained.
   
   
   •  Choose k to be 99% of n (i.e., k = 0.99 ∗ n, rounded to the nearest integer).
   
   
   •  Choose the value of that minimizes the approximation error 
   
   
   •  Choose k to be the largest value so that at least 99% of the variance is retained
   
   
   •  Use the elbow method.
   
   
   •  Choose k to be 99% of m (i.e., k = 0.99 ∗ m, rounded to the nearest integer).
   
   

3. Suppose someone tells you that they ran PCA in such a way that “95% of the variance was retained.” What is an equivalent statement to this?
   
   
   •  
   
   
   •  
   
   
   •     ANSWER
   
   
   •  
   
   
   •  
   
   
   •  
   
   
   •  
   
   
   •  

---

4. Which of the following statements are true? Check all that apply.
   
   
   •  Given only  and , there is no way to reconstruct any reasonable approximation to .
   
   
   •  Even if all the input features are on very similar scales, we should still perform mean normalization (so that each feature has zero mean) before running PCA.

     
     

   •  Given input data , it makes sense to run PCA only with values of k that satisfy . (In particular, running it with  is possible but not helpful, and  does not make sense.)
   •  PCA is susceptible to local optima; trying multiple random initializations may help.
   
   
   •  PCA can be used only to reduce the dimensionality of data by 1 (such as 3D to 2D, or 2D to 1D).
   
   
   •  Given an input , PCA compresses it to a lower-dimensional vector .
   
   
   •  If the input features are on very different scales, it is a good idea to perform feature scaling before applying PCA.

     
     

   •  Feature scaling is not useful for PCA, since the eigenvector calculation (such as using Octave’s svd(Sigma) routine) takes care of this automatically.
   • 
     
   • 5.Which of the following are recommended applications of PCA? Select all that apply.
   • 
     
     •  To get more features to feed into a learning algorithm.
     
     
     •  Data compression: Reduce the dimension of your data, so that it takes up less memory / disk space.

        Preventing overfitting: Reduce the number of features (in a supervised learning problem), so that there are fewer parameters to learn.

     
     
     •  Data visualization: Reduce data to 2D (or 3D) so that it can be plotted.

       
       

     •  Data compression: Reduce the dimension of your input data , which will be used in supervised learning algorithm (i.e., use PCA so that your supervised learning algorithm runs faster ).
     •  As a replacement for (or alternative to) linear regression: For most learning applications, PCA and linear regression give sustantially similar results.
     
     
     •  Data visualization: To take 2D data, and find a different way of plotting it in 2D (using k=2)
   • • 一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
     •  Machine Learning Coursera-All weeks solutions [Assignment + Quiz]   click here

                                                                                     &
                              Coursera Google Data Analytics Professional Quiz Answers   click here
     
     
     
     
     Have no concerns to ask doubts in the comment section. I will give my best to answer it.

     If you find this helpful kindly comment and share the post.

     This is the simplest way to encourage me to keep doing such work.

     
     

     
     

     Thanks & Regards,

     - Wolf
   •